高校受験の数学の問題に必ずと言って出題されるのが,立体を斜めに切断した場合の体積
簡単な公式があるので,それを覚えて臨めばいいのですが,きちんと証明されているサイトがないので考えてみました.
・円柱
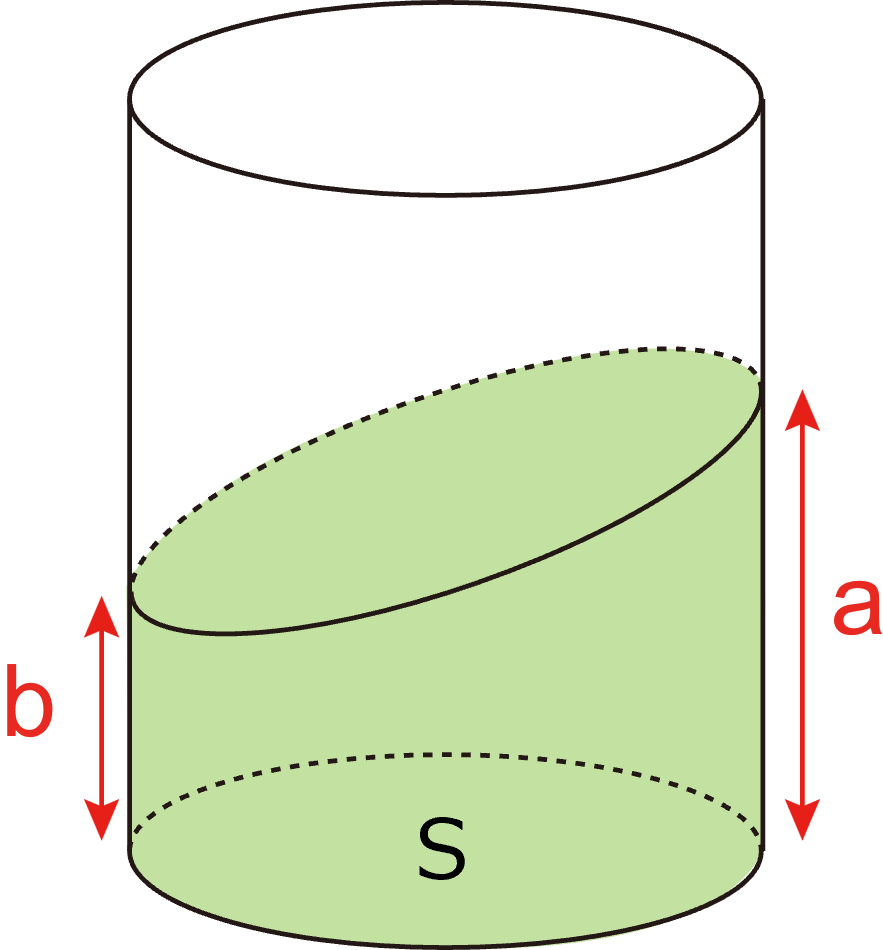
まずは,一番簡単な円柱を斜めに切断した場合の体積です.

高さaと高さbで切断するのですが,切断するのですから当然ながら切断面は平面.底面積をSとします.
底面積に平行な面を考えます.高さはaとbの平均となります.
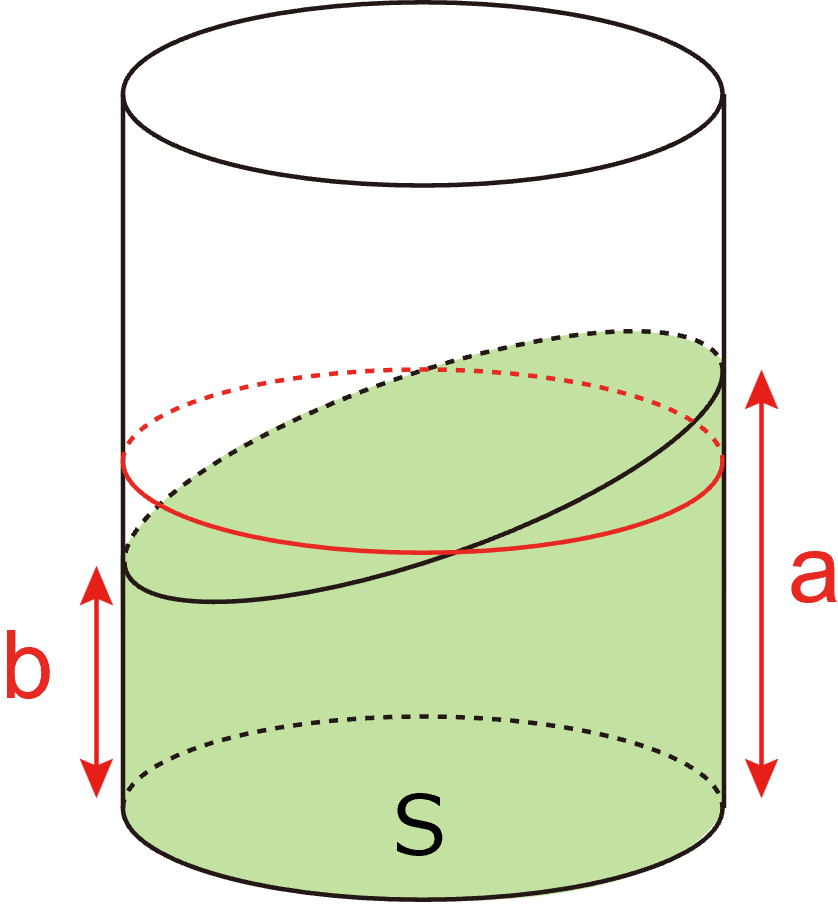
すると,
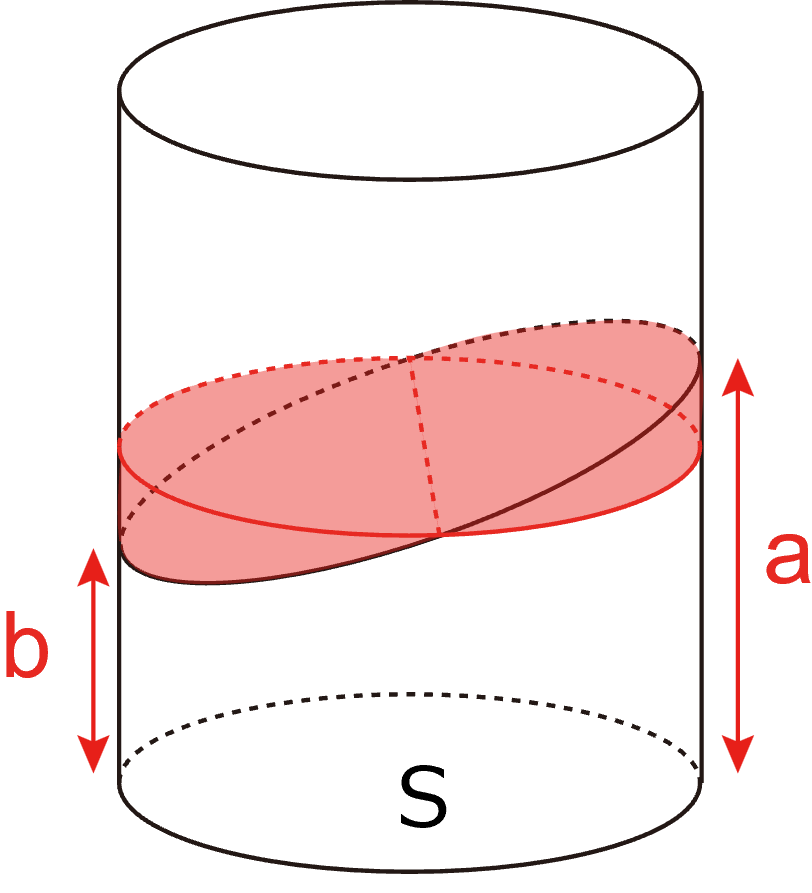
ちょうど,aのエリアの平行な面からはみ出した部分とbのエリアの平衡から下がった部分の体積は等しいので,結果として,
\( \Large \displaystyle V = S \cdot \frac{a+b}{2} \)
となります.これは簡単,次は三角柱です.